Comp578 Susan Portugal Fall 2008
Assignment 7 October 16, 2008
6.10.1
For each of the following questions, provide an example of an association rule from the market basket domain that satisfies the following conditions. Also, describe whether such rules are subjectively interesting.
(a) A rule that has high support and high confidence.
Support is how often a rule is applicable for the provided data set.
Support, s( X → Y ) = [σ( X U Y )] / N
Confidence is how frequently an item in Y appear in transactions that contain X.
Confidence, c( X → Y ) = [σ(X U Y)] / [σ( X )]
High Support and High Confidence
X = Milke
Y = Diapers
{Milk} → {Diapers}
Support = 3/5 = 60%
Confidence = 3/4 = 0.75%
Such rules are not subjectively interesting due to any household that has children would use milk and diapers.
(b) A rule that has reasonably high support but low confidence.
X = Milk
Y = Cola
{Milk} → {Cola}
Support = 2/5 = 40%
Confidence = 2/4 = 50%
Such rule can be interesting besides the fact that both products are liquid that can be consumed, although one is a healthy drink well the other is a high sugar drink.
(c) A rule that has low support and low confidence.
X = Bread
Y = Eggs
{Bread} →{Eggs}
Support = 1/5 = 20%
Confidence = ¼ = 25%
Such rule set is not subjectively interesting due to both items are staple foods.
(d) A rule that has low support and high confidence.
X = Eggs
Y = Diapers
{Eggs} →{Diapers}
Support = 1/5 = 20%
Confidence = 1/1 = 100%
Such rule set is subjectively interesting due to its not being expected.
6.10.2
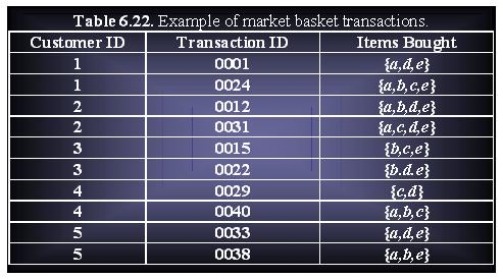
Consider the data set shown in Table 6.22.
(a) Compute the support for items {e}, {b,d}, {b,d,e} by treating each transaction ID as a market basket.
● {e}: support → 8/10 = 80%
● {b,d}: support → 2/10 = 20%
● {b,d,e}: support → 2/5 = 20%
(b) Use the results in part (a) to compute the confidence for the association rules {b,d} → {e} and {e} →{b,d}. Is confidence a symmetric measure?
● {b,d} → {e}: confidence → 2/2 = 100%
● {e} →{b,d}: confidence → 2/8 = 25%
Confidence is not a symmetric measurement.
(c) Repeat part (a) by treating each customer ID as a market basket. Each item should be treated as a binary variable. (1 if an item appears in at least one transaction bought by the customer, and 0 otherwise.)
● {e}: support → 4/5 = 80%.
● {b,d}: support → 5/5 = 100%
● {b,d,e}: support → 4/5 = 80%
(d) Use the results in part (c) to compute the confidence for the association rules {b,d} →{e} and {e} →{b,d}.
● {b,d} → {e}: confidence → 4/5 = 80%
● {e} →{b,d}: confidence → 4/4 = 100%
(e) Suppose s1 and c1 are the support and confidence values of an association rule r when treating each transaction ID as a market basket. Also, let s2 and c2 be the support and confidence values of r when treating each customer ID as a market basket. Discuss whether there are any relationships between s1 and s2 or c1 and c2.
There is a relationship present between s1 and s2 as well as c1 and c2. As each individual item within the data set increase so does the support for a rule as well as the confidence. Therefore s2 and c2 is greater than or equal to s1 and c1 respectively.
6.10.14
Answer the following questions using the data sets shown in Figure 6.34. Note that each data set contains 1000 items and 10,000 transactions. Dark cells indicate the presence of items and white cells indicate the absence of items. We will apply the Apriori algorithm to extract frequent itemsets with minsup = 10% (i.e., itemsets must be contained in at least 1000 transactions)?
(a) Which data set(s) will produce the most number of frequent itemsets?
The data sets that will produce the most number of frequent are (a) and (b).
(b) Which data set(s) will produce the fewest number of frequent itemsets?
The data sets that will produce the fewest number of frequent itemsets are (d) and (f).
(c) Which data set(s) will produce frequent itemsets with highest maximum support?
The data set that will produce frequent itemsets with highest maximum support is (c).
(d) Which data set(s) will produce frequent itemsets with highest maximum support?
The data set that will produce frequent itemsets with highest maximum support is data set (b).
(e) Which data set(s) will produce frequent itemsets containing items with wide-varying support levels (i.e. items with mixed support, ranging fromr less than 20% to more than 70%).
The data set that will produce the frequent itemsets that contains items with wide-varying support levels is data set (e).