Comp578 Susan Portugal Fall 2008
Assignment 3 September 18, 2008
2.6.18
This exercise compares and contrasts some similarity and distance measures.
(a) For binary data, the L1 distance corresponds to the Hamming disatnce; that is, the number of bits that are different between two binary vectors. The Jaccard similarity is a measure of the similarity between two binary vectors. Compute the Hamming distance and the Jaccard similarity between the following two binary vectors.
x = 010101001
y = 010011000
Hamming distance = 3; there are 3 binary numbers different between the x and y.
x = 0101010001
y = 0100011000
Jaccard coefficient: J= (number of matching presences) / (number of attributes not involved in 00 matches)
J=(f11)/(f01 + f10 + f11)
f01 = 1 the number of attributes where x was 0 and y was 1
f10 = 2 the number of attributes where x was 1 and y was 0
f00 = 5 the number of attributes where x was 0 and y was 0
f11 = 2 the number of attributes where x was 1 and y was 1
J= (2) / (1 + 2 + 2)
J = 2/5 = 0.4
(b) Which approach, Jaccard or Hamming distance, is more similar to the Simple Matching Coefficient, and which approach is more similar to the cosine measure? Explain. (Note: The Hamming measure is a distance, while the other three measures are similarities, but don't let this confuse you.)
In comparing the four methods of comparison, in groups of two, the Jaccard coefficient is similar to the Cosine Similarity, the Hamming distance is similar to the Simple Matching Coefficient.
The Jaccard coefficient is a similar method of comparison to the Cosine Similarity due to how both methods compare one type of attribute distributed among all data. The Jaccard approach looks at the two data sets and finds the incident where both values are equal to 1. So the resulting value reflects how many 1 to 1 matches occur in comparison to the total number of data points. This is also known as the frequency that 1 to 1 match, which is what the Cosine Similarity looks for, how frequent a certain attribute occurs.
The Hamming distance is similar to the Simple Matching Coefficient in which both methods look at the whole data and looks for when data points are similar and dissimilar one to one. The Hamming distance gives the result of how many attributes where different. The Simple Matching Coefficient gives the result of the ratio of how many attributes were the same over the entirety of the sample set. The resulting information reveals the same information, one reveals how many were different, the other reveals how many were same, and therefore one reveals the inverse information of the other.
Simple Matching Coefficient: SMC = (f11 + f00) / (f01 + f10 + f11 + f00) = (2 + 5) / (1 + 2 +2 +5) = 7/10 = 0.7
Hamming distance = 3 out of a sample set of 10
(c) Suppose that you are comparing how similar two organisms of different species are in terms of the number of genes they share. Describe which measure, Hamming or Jaccard, you think would be more appropriate for comparing the genetic makeup of two organisms. Explain. (Assume that each animal is represented as a binary vector, where each attribute is 1 if a particular gene is present in the organism and 0 otherwise.)
When comparing if two organisms of similar species the important genes to compare are the alike genes. In the example below when comparing two organisms represented by a binary vector with an attribute of 1 indicating the gene is present; there are 2 genes that are alike out of 10.
x = (0,0,0,1,1,1,0,0,1,0)
y = (1,0,0,1,0,0,1,0,1,1)
This approach of comparison is known as Jaccard Coefficient. The only genes that are important are the alike genes that are that are present. Genes that are not present in either organism does not support that the two organisms are similar.
(d) If you wanted to compare the genetic makeup of two organisms of the same species, e.g., two human beings, would you use the Hamming distance, the Jaccard coefficient, or a different measure of similarity or distance? Explain. (Note that two human beings share > 99.9% of the same genes.)
Since the genes of the two humans are 99.9% alike genes, the only genes of interest are ones that different. The Hamming distance approach only looks at incidents at are different. For example human x and y represented as binary vectors, where each attribute of a gene present is a 1 and otherwise 0 if the gene is not present.
x = (1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0, 1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0, 1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0, 1,1,1,1,0,0,0,1,1,0)
y = (1,1,1,1,0,1,0,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0, 1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0, 1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,0, 1,1,1,1,0,0,0,1,1,0)
The Hamming distance results 1, one difference out of 100 attributes revealing that 99 genes are the same. (This does not represent that 99.99% genes correlate due to simplicity—10000 genes compared with 0 or 1 and one different attribute would reveal that 99.99% are the same.)
2.6.19
For the following vectors, x and y, calculate the indicated similarity or distance measures.
(a) x = (1,1,1,1), y = (2,2,2,2) cosine, correlation, Euclidean
Cosine
x ● y = 1*2 + 1*2 + 1*2 + 1*2 = 8
||x|| = sqrt(1*1 + 1*1 + 1*1 + 1*1) = sqrt (4) = 2
||y|| = sqrt(2*2 + 2*2 + 2*2 + 2*2) = sqrt (16) = 4
cos(x,y) = (x ● y) / (||x||*||y||) = (8)/ (2*4)
cos(x,y) = 1
Correlation
corr(x, y) = [covariance(x,y)] / [standard deviation(x) * standard deviation(y)]
Mean of x =(1+1+1+1) / 4 = 1
Mean of y = (2+2+2+2) / 4 = 2
covariance(x,y) = 1/(4 -1) [(1-1)(2-2) + (1-1)(2-2) + (1-1)(2-2) + (1-1)(2-2)] = 0
Standard deviation (x) = sqrt[((1/(4-1))) * {(1-1)^2 + (1-1)^2 + (1-1)^2 + (1-1)^2}] = sqrt[(1/3) * 0] = 0
Standard deviation (y) = sqrt[((1/(4-1))) * {(2-2)^2 + (2-2)^2 + (2-2)^2 + (2-2)^2}] = sqrt[(1/3) * 0] = 0
corr(x,y) = 0/0 = undefined
Euclidean
d(x, y) = sqrt((1-2)^2 + (1-2)^2 + (1-2)^2 + (1-2)^2)
Euclidean distance = 2
(b) x = (0,1,0,1), y = (1,0,1,0) cosine, correlation, Euclidean, Jaccard
Cosine
x ● y = 0*1 + 1*0 + 0*1 + 1*0 = 0
||x|| = sqrt(0*0 + 1*1 + 0*0 + 1*1) = sqrt (2)
||y|| = sqrt(1*1 + 0*0 + 1*1 + 0*0) = sqrt (2)
cos(x,y) = (x ● y) / (||x||*||y||) = (0)/ (sqrt (2) *sqrt (2))
cos(x,y) = 0
Correlation
corr(x, y) = [covariance(x,y)] / [standard deviation(x) * standard deviation(y)]
Mean of x = (0+1+0+1) / 4 = ½ = 0.5
Mean of y = (1+0+1+0) / 4 = ½ = 0.5
Covariance(x,y) = 1/(4-1) * [(0-½)(1-½) + (1-½)(0-½) +(0-½)(1-½) +(1-½)(0-½) ]
Covariance(x,y) = (1/3) * [(-1/4) + (-1/4) + (-1/4) + (-1/4)]
Covariance(x,y) = -1/3
Standard_deviation (x) = sqrt[((1/(4-1))) * {(1-1/2)^2 + (0-1/2)^2 + (1-1/2)^2 + (0-1/2)^2}] = sqrt[(1/3) * 1] = 0.57735
Standard_deviation (y) = sqrt[((1/(4-1))) * {(0-1/2)^2 + (1-1/2)^2 + (0-1/2)^2 + (1-1/2)^2}] = sqrt[(1/3) * 1] = 0.57735
Corr(x,y) = (-1/3) / (0.57735 * 0.57735)
Corr(x,y) = -1
Euclidean
d(x, y) = sqrt((0-1)^2 + (1-0)^2 + (0-1)^2 + (1-0)^2)
Euclidean distance = 2
Jaccard
J= (numbar of matching presences) / (number of attributes not involved in 00 matches)
J=(f11)/(f01 + f10 + f11)
f01 = 2 the number of attributes where x was 0 and y was 1
f10 = 2 the number of attributes where x was 1 and y was 0
f00 = 0 the number of attributes where x ws 0 and y was 0
f11 = 0 the number of attributes where x was 1 and y was 1
J= (0) / (2 + 2 + 0)
J = 0
(c) x = (0,-1,0,1), y = (1,0,-1,0) cosine, correlation, Euclidean
Cosine
x ● y = 0*1 + (-1)*0 + 0*(-1) + 1*0 = 0
||x|| = sqrt(0*0 + (-1)*(-1) + 0*0 + 1*1) = sqrt (2)
||y|| = sqrt(1*1 + 0*0 + (-1)*(-1) + 0*0) = sqrt (2)
cos(x,y) = (x ● y) / (||x||*||y||) = (0)/ (sqrt (2) *sqrt (2))
cos(x,y) = 0
Correlation
corr(x, y) = [covariance(x,y)] / [standard deviation(x) * standard deviation(y)]
Mean of x = (0+(-1)+0+1) / 4 = 0
Mean of y = (1+0+(-1)+0) / 4 = 0
Covariance(x,y) = 1/(4-1) * [(0-0)(1-0) + (-1-0)(0-0) +(0-0)(-1-0) +(1-0)(0-0) ] = (1/3) * 0 = 0
corr(x,y) = 0
Eulidean
d(x, y) = sqrt((0-1)^2 + (-1-0)^2 + (0+1)^2 + (1-0)^2)
Euclidean distance = 2
(d) x = (1,1,0,1,0,1), y = (1,1,1,0,0,1) cosine, correlation, Jaccard
Cosine
x ● y = 1*1 + 1*1 + 0*1 + 1*0 + 0*0 + 1*1 = 3
||x|| = sqrt(1*1 + 1*1 + 0*0 + 1*1 + 0*0 + 1*1) = 2
||y|| = sqrt(1*1 + 1*1 + 1*1 + 0*0 + 0*0 + 1*1) = 2
cos(x,y) = (x ● y) / (||x||*||y||) = (3)/ (2 * 2)
cos(x,y) = ¾ = 0.75
Correlation
corr(x, y) = [covariance(x,y)] / [standard deviation(x) * standard deviation(y)]
Mean of x = (1+1+0+1+0+1) / 6 = 4/6
Mean of y = (1+1+1+0+0+1) / 6 = 4/6
Covariance(x,y) = 1/(6-1) * [(1-4/6)(1-4/6) + (1-4/6)(1-4/6) +(0-4/6)(1-4/6) +(1-4/6)(0-4/6) + (0-4/6)(0-4/6) + (1-4/6)(1-4/6) ] = (1/5)(1/3)=1/15
Standard_deviation (x) = sqrt[((1/(6-1))) * {(1-4/6)^2 + (1-4/6)^2 + (0-4/6)^2 + (1-4/6)^2 + (0-4/6)^2 + (1-4/6)^2}] = sqrt[(1/5) * (4/3)] = 0.5164
Standard_deviation (y) = sqrt[((1/(6-1))) * {(1-4/6)^2 + (1-4/6)^2 + (1-4/6)^2 + (0-4/6)^2 + (0-4/6)^2 + (1-4/6)^2}] = sqrt[(1/5) * (4/3)] = 0.5164
Corr(x,y) = (1/15) / (0.5164 * 0.5164)
Corr(x,y) = 0.25
Jaccard
J= (numbar of matching presences) / (number of attributes not involved in 00 matches)
J=(f11)/(f01 + f10 + f11)
f01 = 1 the number of attributes where x was 0 and y was 1
f10 = 1 the number of attributes where x was 1 and y was 0
f00 = 1 the number of attributes where x ws 0 and y was 0
f11 = 3 the number of attributes where x was 1 and y was 1
J= (3) / (1 + 1 + 3)
J = 3/5 = 0.6
(e) x = (2,-1,0,2,0,-3), y = (-1,1,-1,0,0,-1) cosine, correlation
Cosine
x ● y = 2*(-1) + (-1)*1 + 0*(-1) + 2*0 + 0*0 + (-3)*(-1) = 0
||x|| = sqrt(2*2 + (-1)*(-1) + 0*0 + 2*2 + 0*0 + (-3)*(-3)) = sqrt (18)
||y|| = sqrt((-1)*(-1) + 1*1 + (-1)*(-1) + 0*0 + 0*0 + (-1)*(-1)) = 2
cos(x,y) = (x ● y) / (||x||*||y||) = (0)/ (sqrt (18) * 2)
cos(x,y) = 0
Correlation
corr(x, y) = [covariance(x,y)] / [standard deviation(x) * standard deviation(y)]
Mean of x = (2+(-1)+0+2+0+(-3)) / 6 = 0
Mean of y = ((-1)+1+(-1)+0+0+(-1)) / 6 = -1/6
Covariance(x,y) = 1/(6-1) * [(2-0)(-1+1/6) + (-1-0)(1+1/6) +(0-0)(-1+1/6) + (2-0)(0+1/6) + (0-0)(0+1/6) + (-3-0)(-1+1/6) ] = (1/5) * 0 = 0
Corr(x,y) = 0
3.6.1
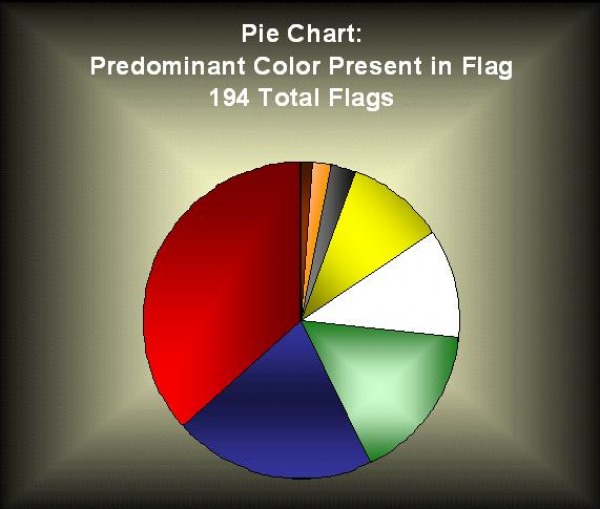
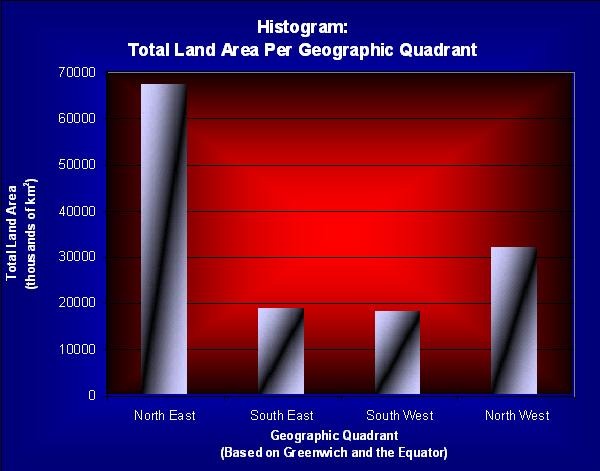
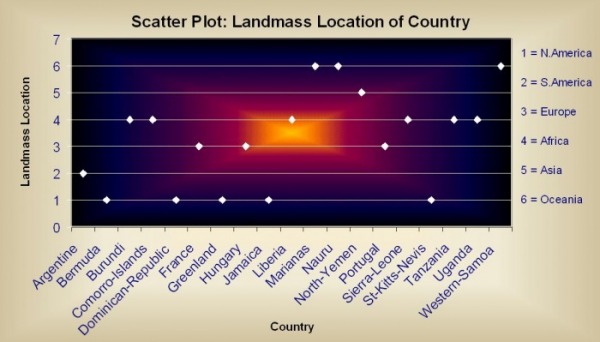
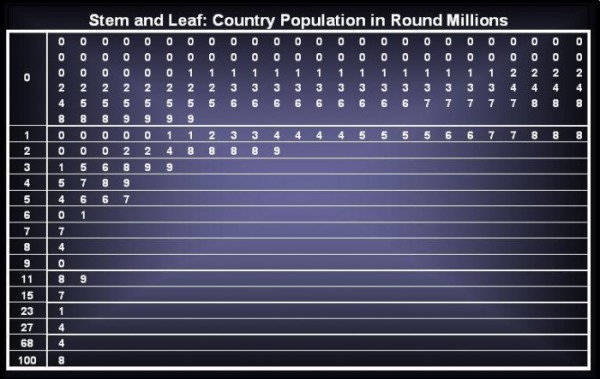
Obtain one of the data sets available at the UCI Machine Learning Repository and apply as many of the different visulization techniques described in the chapter as possible. The bibliographic notes and book Web site provide pointers to visualization software.
The data set obtained at the UCI Machine Learning Repository website pertained to the attributes of various Countries in the world, concentrating on each Country Flag. The data set obtain is represented below in four different methods: Pie Chart, Histogram, Scatter Plot, and Stem and Leaf. ( http://archive.ics.uci.edu/ml/datasets/Flags )
References:
Introduction to Data Mining,By: Pang-Ning Tan, Michael Steinbach, Vipin Kumar - Addison Wesley,2005,0321321367
UCI machine Learing Repository: Flag Data Set http://archive.ics.uci.edu/ml/datasets/Flags